SOAL PERSAMAAN LOGARITMA DAN SIFAT-SIFATNYA
Sifat-Sifat Logaritma
Sifat-sifat Logaritma
Operasi logaritma memiliki sifat apabila dikalikan, dibagi, ditambah, dikurang atau bahkan dipangkatkan. Sifat-sifat dari operasi logaritma tersebut dijelaskan oleh tabel di bawah ini :

1. Sifat Logaritma Dasar
Sifat dasar dari sebuah perpangkatan adalah apabila sebuah bilangan dipangkatkan dengan 1 maka hasilnya akan tetap sama dengan sebelumnya.
Sama halnya dengan logaritma, apabila sebuah logaritma memiliki basis dan numerus yang sama maka hasilnya adalah 1.
a log a = 1
Selain itu, apabila suatu bilangan dipangkatkan dengan 0 maka hasilnya adalah 1. Untuk itulah apabila numerus logaritma bernilai 1 maka hasilnya adalah 0.
a log 1 = 0
2. Logaritma Koefisien
Apabila sebuah logaritma memiliki basis atau numerus yang berpangkat. Maka, pangkat dari basis atau numerus tersebut dapat menjadi koefisien dari logaritma itu sendiri.
Pangkat basis menjadi penyebut dan pangkat numerus menjadi pembilang.
( a^x ) log ( b^y ) = ( y / x ) . a log b
Ketika basis dan numerus memiliki pangkat yang bernilai sama maka pangkat tersebut dapat dihilangkan karena koefisien logaritma bernilai 1.
(a^x)log(b^x) = (x/x) . a log b = 1 . a log b
Sehingga
(a^x) log (b^x) = a log b
3. Logaritma Sebanding Terbalik
Sebuah logaritma dapat memiliki nilai yang sebanding dengan logaritma lain yang berbanding terbalik antara basis dan numerusnya.
a log b = 1 / ( b log a )
Jangan langsung kesel karena liat sifat-sifat logaritma di atas ya hehehe. Semua sifat logaritma di atas bisa kita kuasai dengan mudah jika kita sering mengerjakan latihan soal logaritma. Ayo kita kerjakan soal-soal dibawah ini.
4. Sifat Perpangkatan Logaritma
Apabila sebuah bilangan dipangkatkan dengan logaritma yang memiliki basis yang sama dengan bilangan tersebut maka hasilnya akan berupa numerus dari logaritma itu sendiri.
a ^ ( a log b ) = b
5. Sifat Penjumlahan dan Pengurangan Logaritma
Logaritma dapat dijumlahkan dengan logaritma lain yang memiliki basis yang sama. Hasil dari penjumlahan tersebut berupa logaritma dengan basis yang sama dan numerus yang dikalikan.
a log x + a log y = a log ( x . y )
Selain penjumlahan, logaritma juga dapat dikurangkan dengan logaritma lain yang memiliki basis yang sama.
Namun, terdapat perbedaan pada hasilnya dimana hasilnya akan berupa pembagian antara numerus dari logaritma.
a log x – a log y = a log ( x / y )
6. Sifat Perkalian dan Pembagian Logaritma
Operasi perkalian antara dua buah logaritma dapat disederhanakan apabila kedua logaritma tersebut memiliki basis atau numerus yang sama.
a log x . x log b = a log b
Sedangkan untuk pembagian logaritma dapat disederhanakan apabila kedua logaritma hanya memiliki basis yang sama.
x log b / x log a = a log b
7. Sifat Logaritma Numerus Terbalik
Sebuah logaritma dapat memiliki nilai yang sama dengan negatif logaritma lain yang memiliki numerus dengan pecahan terbalik.
a log ( x / y ) = – a log ( y / x )
Contoh Latihan Soal Logaritma 1
Contoh Soal 1
²log 16 =….
Contoh Soal 2
Contoh Soal 3
Contoh Soal 4
Jika ³log 2 = a, maka ³log 6 =….
Pembahasan :
Contoh Soal Logaritma 2
Sederhanakan logaritma berikut ini!
2log 25 .5log 4 +2log 6 –2log 39log 36 /3log 79^(3log 7)
Jawab :
a. 2 log 25 . 5 log 4 + 2 log 6 – 2log 3
= 2 log 52 . 5 log 22 + 2 log (3.2/3)
= 2.2 . 2 log 5 . 5 log 2+ 2 log 2
= 2 . 2 log 2 + 1
= 2 . 1 + 1
= 3
b. 9 log 4 / 3 log 7
= 3^2 log 22 / 3 log 7
= 3 log 2 / 3 log 7
= 7 log 2
c. 9^(3 log 7)
= 32 ^(3 log 7)
= 3^(2 .3 log 7)
= 3^(3 log 49)
= 49

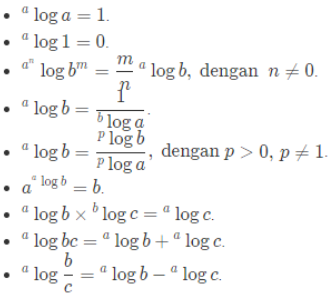


Tidak ada komentar:
Posting Komentar