Eksponensial selain dalam ilmu matematika sering digunakan dari berbagai bidang ekonomi, biologi, dan kimia selain itu juga sebagai ilmu komputer dengan aplikasi yang saling berhubungan pada kinerja ilmu matematika dan kimia. Fungsi Eksponensial dalam logaritma yang terkait dengan erat serta memiliki aplikasi penting dalam perekonomian yang berkaitan dengan masalah pertumbuhan yang di mana ekonomi secara umum.
Konsep :
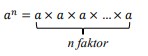
Dengan :
a = Bilangan pokok
n = Bilangan pangkat/eksponen
Sifat Bilangan Eksponensial.
Dengan π > 0 dan π ≠ 0
Fungsi eksponensial f dengan bilangan pokok a adalah fungsi yang memetakan setiap bilangan real x ke ππ₯ dengan π > 0 dan π ≠ 1 dan ditulis sebagai :
- Bentuk pemetaan : f : π₯ → ππ₯ , dengan π > 0 dan π ≠ 1 atau
- Bentuk formula : π(π₯) = π π₯ , dengan π > 0 dan π ≠ 1
1 – 10 Contoh Soal Fungsi Eksponensial dan Jawaban
1. Diberikan π(π₯) = 22π₯−1 , carilah nilai dari π(2) dan π ( ½ )
Jawaban :
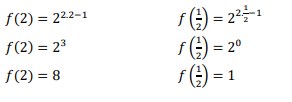
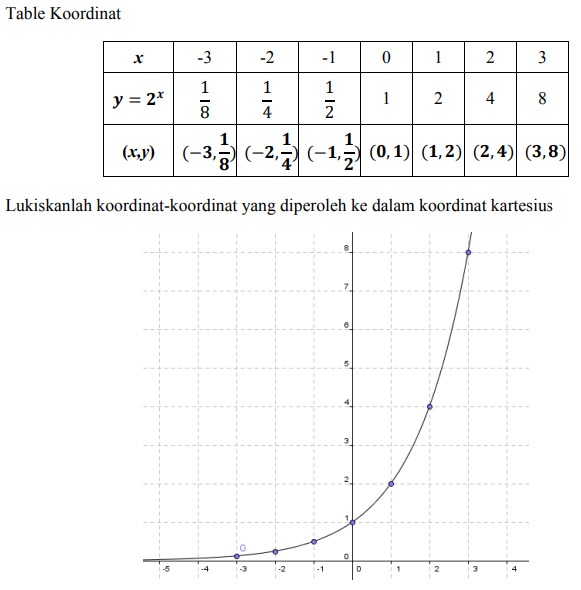
2. Lukislah grafik fungsi π¦ = 2π₯ dengan π₯ ∈ R
Jawaban :
3. Nilai x yang memenuhi persamaan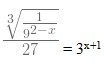 
adalah . . .
A. -16
B. -7
C. 4
D. 5
E. 6
Jawaban : A
Pembahasan :
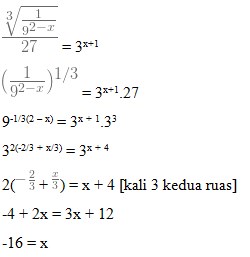
4. √15 + √60 – √27 = …
Jawaban :
√15 + √60 – √27
= √15 + √(4×15) – √(9×3)
= √15 + 2√15 – 3√3
= 3√15 – 3√3
= 3(√15 – √3)
5. Perhatikanlah ilustrasi berikut ini
Tentukanlah himpunan penyelesaian dari | x – 2014 | ≤ 6
Jawaban :
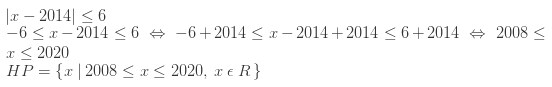
Simak Juga : Soal Persamaan Garis Lurus Pilihan Ganda
6. Gambarkanlah grafik
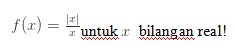
Jawaban :
dan seterusnya
Perhatikanlah ilustrasi berikut ini
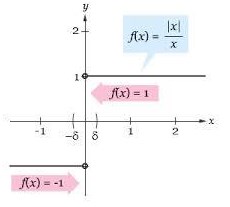
7. Bentuk sederhana dari ( 1 + 3√2) – ( 4 – √50 ) adalah ….
A. – 2√2 – 3
B. – 2√2 + 5
C. 8 √2 – 3
D. 8 √2 + 3
E. 8 √2 + 5
Jawaban : C
Pembahasan :
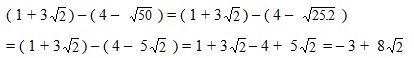
8. Jika 2log 3 = a dan 3log 5 = b, maka 15log 20 = ….
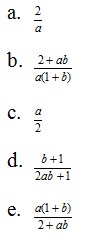
Jawaban : B
Pembahasan :
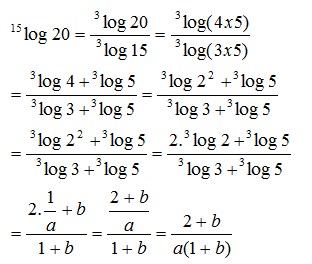
9. Nilai dari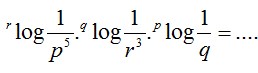 
A. – 15
B. – 5
C. – 3
D. 1/15
E. 5
Jawaban : A
Pembahasan :
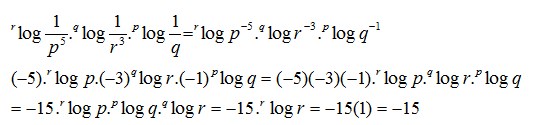
10. Nilai dari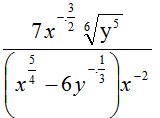 
untuk x = 4 dan y = 27 adalah ….
A. (1 + 2√2 ) 9√2
B. (1 + 2√2 ) 9√3
C. (1 + 2√2 ) 18√2
D. (1 + 2√2 ) 27√2
E. (1 + 2√2 ) 27√3
Jawaban : B
Pembahasan :
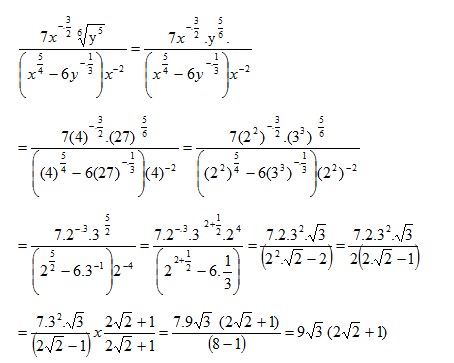
11 – 20 Contoh Soal Fungsi Eksponensial dan Jawaban
11. Akar – akar persamaan 32x+1 – 28.3x + 9 = 0 adalah x1 dan x2. Jika x1 > x2, maka nilai 3x1 – x2= …
A. – 5
B. – 1
C. 4
D. 5
E. 7
Jawaban : E
Pembahasan :
12. Akar – akar persamaan 2.34x – 20.32x + 18 = 0 adalah x1 dan x2. Nilai x1 + x2 = ….
A. 0
B. 1
C. 2
D. 3
E. 4
Jawaban :
Pembahasan :
Caranya sama dengan nomor 12, tetapi yang dimisalkan adalah 32x
Silahkan dicoba ya Soal Fungsi Eksponensial . . .
13. Nilai x yang memenuhi persamaan 22log (2x+1+ 3) = 1 + 2log x adalah ….
A. 2log 3
B. 3log 2
C. – 1 atau 3
D. 8 atau ½
E. log 2/3
Jawaban : A
Pembahasan :
2log.2log (2x+1 + 3) = 1 + 2log x
2log.2log (2x+1 + 3) = 2log 2 + 2log x
2log.2log (2x+1 + 3) = 2log 2x ( gunakan kesamaan pada logaritma )
2log (2x+1 + 3) = 2x ( gunakan definisi logaritma sebagai invers eksponen alog b = c ↔ b= ac )
2x+1 + 3 = 22x ( pindahkan semua nilai ke ruas kanan )
22x – 2x+1 – 3 = 0
(2x)2 – 2x.21 – 3 = 0
(2x)2 – 2.2x – 3 = 0
Misal 2x = q
q2 – 2q – 3 = 0
( q – 3 ) ( q + 1 ) = 0
q – 3 = 0 atau q + 1 = 0
q = 3 atau q = –1
substitusikan nilai q pada 2x = q
2x = 3 atau 2x = –1
x = 2log 3 (untuk 2x = –1 tidak ada nilai x yang memenuhi, sebab hasil dari suatu bilangan yang dipangkatkan tidak pernah negatif )
14. Penyelesaian pertidaksamaan log (x – 4) + log (x + 8) < log (2x + 16) adalah ….
A. x > 6
B. x > 8
C. 4 < x < 6
D. – 8 < x < 6
E. 6 < x < 8
Jawaban : C
Pembahasan Soal Fungsi Eksponensial :
log (x – 4) + log (x + 8) < log (2x + 16)
log (x – 4) (x + 8) < log (2x + 16)
log ( x2 + 4x – 32 ) < log ( 2x + 16 ) (gunakan kesamaan pada logaritma)
( x2 + 4x – 32 ) < ( 2x + 16 )
x2 + 4x – 32 – 2x – 16 < 0
x2 + 2x – 48 < 0
( x + 8 ) ( x – 6 ) < 0 (daerah Himpunan Penyelesaian ke – 1 )
Cari harga pembuat nol untuk ( x + 8 ) dan ( x – 6 ), didapat x = –8 dan x = 6
Selain daerah penyelesaian diatas sebagai jawaban perlu juga dicek kembali nilai numerus untuk logaritmanya.
Untuk log (x – 4), nilai x – 4 > 0
x > 4 ( daerah Himpunan Penyelesaian ke – 2 )
Untuk log (x + 8), nilai x + 8 > 0
x > –8 ( daerah Himpunan Penyelesaian ke – 3 )
Untk log (2x + 16), nilai 2x + 16 > 0
x > –8 ( daerah Himpunan Penyelesaian ke – 4 )
Cat : Untuk mendapatkan daerah positif atau negatif pada HP 1 caranya dengan substitusi nilai yang berada pada daerah tertentu, misalnya nilai yang kurang dari -8 ( misalnya diambil -9)
Substitusi nilai tersebut pada persamaan x2 + 2x – 48
F(-9) = (-9)2 + 2 (-9) – 48 = 81 – 18 – 48 = 15 ( didapat hasil yang positif )
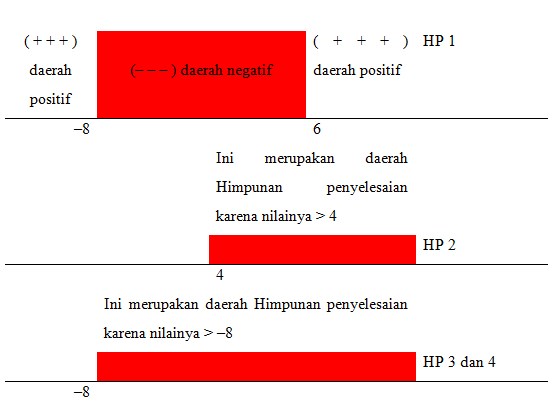
Daerah yang memeuhi ketiga HP diatas adalah irisan dari ketiga HP tersebut, yaitu 4 < x < 6
15. Nilai x yang memenuhi pertidaksamaan : 2 log x log (2x + 5) + 2 log 2 adalah ….
A. -5/2 < x ≤ 8
B. -2 ≤ x ≤ 10
C. 0 < x ≤ 10
D. -2 < x < 0
E. -5/2 ≤ x < 0
Jawaban : C
Pembahasan :
2 log x log (2x + 5) + 2 log 2
log x2 log (2x + 5) + log 22
log x2 log (2x + 5) ( 4 ) ( gunakan kesamaan pada logaritma )
x2 (2x + 5) ( 4 )
x2 8x + 20
x2 – 8x – 20 0
( x – 10 ) ( x + 2 ) 0
Cari harga pembuat nol untuk ( x + 2 ) dan ( x – 10 ), didapat x = –2 dan x = 10
Selain daerah penyelesaian diatas sebagai jawaban perlu juga dicek kembali nilai numerus untuk logaritmanya.
Untuk log x, nilai x > 0 (daerah Himpunan Penyelesaian ke – 2 )
Untuk log ( 2x + 5 ), nilai 2x + 8 > 0 x > – 5/2 ( daerah Himpunan Penyelesaian ke – 3 )
Daerah yang memeuhi ketiga HP diatas adalah irisan dari ketiga HP tersebut, yaitu 0 < x ≤ 10
Lihat Juga : Contoh Soal Bilangan Palindrom
16. Himpunan penyelesaian persamaan 2.9x – 3x+1 + 1 = 0 adalah ….
A. { ½ , 1 }
B. { –½ , –1 }
C. { –½ , 1 }
D. { 0 , 3log ½ }
E. { ½ , ½log 3 }
Jawaban :
Pembahasan :
Caranya sama dengan sebelumnya, tetapi yang dimisalkan adalah 32x.
17. Nilai x yang memenuhi pertidaksamaan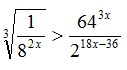 
adalah …
A. x < –14
B. x < –15
C. x < –16
D. x < –17
E. x < –18
Jawaban : E
Pembahasan :
18. Himpunan penyelesaian persamaan xlog ( 10x3 – 9x ) = xlog x5 adalah ….
A. { 3 }
B. { 1,3 }
C. { 0,1,3 }
D. { –3, –1,1,3 }
E. { –3, –1,0,1,3 }
Jawaban : B
Pembahasan :
xlog ( 10x3 – 9x ) = xlog x5 ( gunakan kesamaan pada logaritma )
10x3 – 9x = x5
x5 – 10x3 + 9x = 0 ( faktorkan dengan mengeluarkan variabel x)
x ( x4 – 10x2 + 9 ) = 0 ( faktorkan kembali persamaan yang ada didalam kurung )
x ( x2 – 9 ) ( x2 – 1 ) = 0 ( faktorkan kembali persamaan yang ada didalam kurung )
x ( x – 3 ) ( x + 3 ) ( x – 1 ) ( x + 1 ) = 0
Cari harga pembuat nol untuk x, ( x – 3 ), ( x + 3 ), ( x – 1 ) dan ( x + 1 ).
Didapat
x = 0
x = 3
x = –3
x = 1
x = –1
Dari kelima jawaban hanya 1 dan 3 yang memenuhi persyaratan jika disubstitusikan kepersamaan ( ingat kembali syarat dari bilangan pokok logaritma )
19. Nilai x yang memenuhi 3x²-3x+4 adalah ….
A. 1 < x < 2
B. 2 < x < 3
C. –3 < x < 2
D. –2 < x < 3
E. –1 < x < 2
Jawaban Soal Fungsi Eksponensial : B
Pembahasan :
20. Jika x1 dan x2 adalah akar – akar persamaan (3log x)2 – 3.3log x + 2 = 0, maka x1.x2 = ….
A. 2
B. 3
C. 8
D. 24
E. 27
Jawaban : E
Pembahasan :
(3log x)2 – 3.3log x + 2 = 0
Misal 3log x = p
p2 -3p + 2 = 0
( p – 2 ) ( p – 1 ) = 0
p1 = 2 atau p2 = 1
3log x1 = 2 atau 3log x2 = 1
x1 = 9 atau x2 = 3
x1 . x2 = 27
Tidak ada komentar:
Posting Komentar