EKSPONEN DAN SIFAT-SIFATNYA

 

EXPONENT RULES

Exponent rules, laws of exponent and examples.

• What is an exponent
• Exponents rules
• Exponents calculator

What is an exponent

The base a raised to the power of n is equal to the multiplication of a, n times:

a ⁿ = a × a × ... × a

                    n times

a is the base and n is the exponent.

Examples

3¹ = 3

3² = 3 × 3 = 9

3³ = 3 × 3 × 3 = 27

3⁴ = 3 × 3 × 3 × 3 = 81

3⁵ = 3 × 3 × 3 × 3 × 3 = 243

Exponents rules and properties

Rule name	Rule
Product rules	a n ⋅ a m = a n+m
	a n ⋅ b n = (a ⋅ b) n
Quotient rules	a n / a m = a n-m
	a n / b n = (a / b) n
Power rules	(bn)m = bn⋅m
	bnm = b(nm)
	m√(bn) = b n/m
	b1/n = n√b
Negative exponents	b-n = 1 / bn
Zero rules	b0 = 1
	0n = 0 , for n>0
One rules	b1 = b
	1n = 1
Minus one rule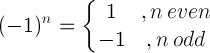
Derivative rule	(xn)' = n⋅x n-1
Integral rule	∫ xndx = xn+1/(n+1)+C

Exponents product rules

Product rule with same base

aⁿ ⋅ a^m = a^n+m

Example:

2³ ⋅ 2⁴ = 2³⁺⁴ = 2⁷ = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

Product rule with same exponent

aⁿ ⋅ bⁿ = (a ⋅ b)ⁿ

Example:

3² ⋅ 4² = (3⋅4)² = 12² = 12⋅12 = 144

See: Multplying exponents

Exponents quotient rules

Quotient rule with same base

aⁿ / a^m = a^n-m

Example:

2⁵ / 2³ = 2^5-3 = 2² = 2⋅2 = 4

Quotient rule with same exponent

aⁿ / bⁿ = (a / b)ⁿ

Example:

4³ / 2³ = (4/2)³ = 2³ = 2⋅2⋅2 = 8

See: Dividing exponents

Exponents power rules

Power rule I

(aⁿ) ^m = a ^n⋅m

Example:

(2³)² = 2^3⋅2 = 2⁶ = 2⋅2⋅2⋅2⋅2⋅2 = 64

Power rule II

_a n^m _= a (n^m)

Example:

₂3² _{= 2}(3²) _{= 2}(3⋅3) _{= 2}9 _{= 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512}

Power rule with radicals

^m√(a ⁿ) = a ^n/m

Example:

²√(2⁶) = 2^6/2 = 2³ = 2⋅2⋅2 = 8

Negative exponents rule

b^-n = 1 / bⁿ

Example:

2^-3 = 1/2³ = 1/(2⋅2⋅2) = 1/8 = 0.125

PERSAMAAN EKSPONEN

SIFAT bx=by  Jika dan Hanya Jika x=y dg b > 0 dan b ≠ 1

42x−1=64  42x−1=43  2x–1=3  2x=4  x=2

SIFAT f(x) g(x) = f(x) g(x) maka: (1) g(x) = h(x), (2) f(x) = 1, (3) f(x) = -1, dengan syarat g(x) dan h(x) sama-sama genap atau ganjil, (4) f (x) = 0, dengan syarat g(x), h(x) > 0.

(x – 2)x^2-2x = (x – 2)x+4, Kondisi (1) nya  x2 – 2x = x + 4  x2 – 3x – 4 = 0  (x – 4)(x + 1) = 0  x = 4 dan x = – 1, Kondisi (2) nya (x – 2) = 1  x – 2 = 1  x = 3, Kondisi (3) nya (x – 2) = – 1  x – 2 = – 1  x = 1, Kondisi (4) nya (x – 2) = 0  x – 2 = 0  x = 2 tetapi karena g(x) > 0  22 – 2.2 = 0 bukan > 0 maka tidak Hp, dari ke-4 kondisi diperoleh Himpunan Penyelesaian x adalah Hp =  {– 1, 1, 3, 4}

SIFAT af(x) = 1 ↔ f(x) = 1, (1)  a = 1 , (2)  a = -1,  dengan syarat f(x) genap, (3)  f(x) = 0,  dengan syarat a ≠ 0

(2x + 3)x – 1  = 1  Kondisi (1) (2x + 3) = 1  2x + 3 = 1  2x = – 2  x = – 1, Kondisi (2) (2x + 3) = – 1  2x + 3 = – 1  2x = – 4  x = – 2 karena  pada  x  - 1 =  – 2 – 1 hasilnya tidak genap maka bukan Hp, Kondisi (3) (x–1) = 0  x – 1 = 0  x = 1   jadi Hp {– 1, 1} 

SIFAT af(x) = bf(x) ↔ f(x) = 0  dengan a, b > 0 dan a, b ≠ 1

3 2x – 2 = 5 x – 1  krn beda pangkat maka ubah jadi sama 3 2(x – 1) = 5x – 1  9 x – 1 = 5 x – 1 dan pangkatnya sudah sama maka  (x–1)=0  x–1=0  x = 1   

SIFAT af(x) = bg(x) ↔ log af(x) = log bg(x)

(2/3)x = 61-x   log (2/3)x = log 6 1 – x   x log (2/3) = (1 - x) log 6 DASARNYA log an = n log a  x log (2/3) = log 6 - x log 6  x log (2/3) + x log 6 = log 6  x (log (2/3) + log 6) = log 6  x log 4 = log 6 DASARNYA  log a + log b = log (ab)  x = log6/log4  x = 4log 6  Jadi, penyelesaiannya adalah x = 4log 6      

SIFAT  p . a 2 f(x) + q . a f(x) + r = 0 dimisalkan a f(x) = L maka persamaannya menjadi p . L 2 + q . L + r = 0

22x - 3. 2x+1 + 8 = 0  22x - 3. 2x+1 + 8 = 0    (2x)2 - 3. 2x . 21 + 8= 0   (2x)2 - 6(2x) + 8 = 0   Misalkan 2x = p, sehingga   p2 - 6p + 8 = 0   (p - 2)(p - 4) = 0  p = 2 atau p = 4   Untuk p = 2   2x = 2  2x = 21    x = 1    Untuk p = 4    2x = 4   2x = 22     x = 2, Jadi, HP = {1, 2}