SOAL EKSPONEN DAN PENYELESAIANNYA

PUTRI DEA ANANDA . X MIPA 1

dari berbagai sumber 

Soal dan Pembahasan – Fungsi Eksponen (Pangkat)

Berikut disajikan sejumlah soal dan pembahasan terkait fungsi eksponen (pangkat) yang dipelajari saat kelas X pada mata pelajaran Matematika Peminatan. Gambar grafik yang disajikan di dalam postingan ini merupakan produk dari penggunaan aplikasi Geogebra.

Soal Nomor 1
Diketahui grafik fungsi $f\left(x\right)=2\cdot 3^{1-x}$. Grafik tersebut melalui titik $\cdots \cdot$
A. $(2,\frac{1}{3})$                   D. $(2,-3)$
B. $(2,\frac{2}{3})$                   E. $(2,-6)$
C. $(2,\frac{4}{3})$

Pembahasan

Berdasarkan opsi yang diberikan, semua titik memiliki absis $x=2$.
Untuk itu, kita uji nilai fungsi saat $x=2$.
Karena $f\left(x\right)=2\cdot 3^{1-x}$, maka
$\begin{array}{cc}f\left(2\right)& =2\cdot 3^{1-2}\\ & =2\cdot 3^{-1}\\ & =\frac{2}{3}\end{array}$
Ini artinya, nilai fungsi saat $x=2$ adalah $y=\frac{2}{3}$. Dengan kata lain, fungsi tersebut melalui titik $(2,\frac{2}{3})$
(Jawaban B)

[collapse]

Soal Nomor 2
Grafik fungsi $f\left(x\right)=k\cdot 2^{5x-8}$ melalui titik $(2,20)$. Nilai $-3k$ adalah $\cdots \cdot$
A. $-15$                  C. $-3$                    E. $15$
B. $-5$                    D. $5$

Pembahasan

Diketahui $f\left(x\right)=k\cdot 2^{5x-8}$.
Karena grafik fungsi melalui titik $(2,20)$, yang artinya $x=2$ dan $y=f\left(2\right)=20$, kita peroleh
$\begin{array}{cc}20& =k\cdot 2^{5\left(2\right)-8}\\ 20& =k\cdot 2^2\\ k& =\frac{20}{4}=5\end{array}$
Dengan demikian, nilai dari $-3k=-3\left(5\right)=-15$
(Jawaban A)

[collapse]

Soal Nomor 3
Grafik fungsi $f\left(x\right)=6^{x+1}+6^{1-x}$ memotong sumbu-$Y$ di titik $\cdots \cdot$
A. $(0,12)$                      D. $(6,0)$
B. $(0,6)$                        E. $(12,0)$
C. $(0,0)$

Pembahasan

Diketahui $f\left(x\right)=6^{x+1}+6^{1-x}$.
Saat grafik fungsi memotong sumbu-$Y$, absis titik yang dilalui fungsi bernilai $0$, ditulis $x=0$.
Untuk itu, kita peroleh
$\begin{array}{cc}f\left(0\right)& =6^{0+1}+6^{1-0}\\ & =6+6=12\end{array}$
Dengan demikian, titik potong grafik fungsi $f\left(x\right)$ terhadap sumbu-$Y$ adalah $(0,12)$
(Jawaban A)

[collapse]

Soal Nomor 4
Jika $f\left(x\right)=2^x$, maka $f(m+n)$ sama dengan $\cdots \cdot$
A. $f\left(m\right)+f\left(n\right)$
B. $f\left(m\right)\cdot f\left(n\right)$
C. $f\left(m\right)-f\left(n\right)$
D. $\frac{f\left(m\right)}{f\left(n\right)}$
E. $\left[f\right(m){]}^{f\left(n\right)}$

Pembahasan

Diketahui $f\left(x\right)=2^x$, sehingga
$\begin{array}{cc}f(m+n)& =2^{m+n}\\ & =2^m\cdot 2^n\\ & =f\left(m\right)\cdot f\left(n\right)\end{array}$
Jadi, hasil dari $f(m+n)=f\left(m\right)\cdot f\left(n\right)$
(Jawaban B)

[collapse]

Soal Nomor 5
Jika $f\left(x\right)=2^x$, maka nilai dari $\frac{f(x+3)}{f(x-1)}=\cdots \cdot$
A. $f\left(2\right)$                    D. $f\left(\frac{x+3}{x-1}\right)$
B. $f\left(4\right)$                    E. $f(2x+2)$
C. $f\left(16\right)$

Pembahasan

Diketahui $f\left(x\right)=2^x$. Ini berarti,
$f(x+3)=2^{x+3}$ dan $f(x-1)=2^{x-1}$.
Oleh karena itu, kita mendapat
$\begin{array}{cc}\frac{f(x+3)}{f(x-1)}& =\frac{2^{x+3}}{2^{x-1}}\\ & =\frac{2^x\cdot 2^3}{2^x\cdot 2^{-1}}\\ & =\frac{2^3}{2^{-1}}=2^3\times 2^1=2^4\end{array}$
Karena $f\left(x\right)=2^x\Rightarrow f\left(4\right)=2^4$, maka hasil dari $\frac{f(x+3)}{f(x-1)}=f\left(4\right)$
(Jawaban B)

[collapse]

Soal Nomor 6
Jika $f\left(x\right)=3^x$, maka $f(a+2b-c)=\cdots \cdot$
A. $f\left(a\right)+f\left(2b\right)-f\left(c\right)$
B. $\frac{2f\left(a\right)\cdot f\left(b\right)}{f\left(c\right)}$
C. $\frac{f\left(a\right)\cdot \left(f\right(b){)}^2}{f\left(c\right)}$
D. $\frac{f\left(a\right)+\left(f\right(b){)}^2}{f\left(c\right)}$
E. $f(a+2b)-f\left(c\right)$

Pembahasan

Diketahui $f\left(x\right)=3^x$, sehingga
$\begin{array}{cc}f(a+2b-c)& =3^{a+2b-c}\\ & =\frac{3^a\cdot 3^{2b}}{3^c}\\ & =\frac{3^a\cdot (3^b{)}^2}{3^c}\\ & =\frac{f\left(a\right)\cdot \left(f\right(b){)}^2}{f\left(c\right)}\end{array}$
Jadi, hasil dari $f(a+2b-c)=\frac{f\left(a\right)\cdot \left(f\right(b){)}^2}{f\left(c\right)}$
(Jawaban C)

[collapse]

Soal Nomor 7
Jika $f\left(x\right)=4^{x+1}$, maka $f(a+b)=\cdots \cdot$
A. $f\left(a\right)\cdot f\left(b\right)$
B. $f\left(a\right)+f\left(b\right)$
C. $4f\left(a\right)\cdot f\left(b\right)$
D. $\frac{1}{4}f\left(a\right)\cdot f\left(b\right)$
E. $\frac{1}{16}f\left(a\right)\cdot f\left(b\right)$

Pembahasan

Diketahui $f\left(x\right)=4^{x+1}$.
Dengan demikian,
$\begin{array}{cc}f(a+b)& =4^{(a+b)+1}\\ & =4^{(a+1)+(b+1)-1}\\ & =4^{a+1}\cdot 4^{b+1}\cdot 4^{-1}\\ & =f\left(a\right)\cdot f\left(b\right)\cdot \frac{1}{4}\\ & =\frac{1}{4}f\left(a\right)\cdot f\left(b\right)\end{array}$
Jadi, hasil dari $f(a+b)=\frac{1}{4}f\left(a\right)\cdot f\left(b\right)$
(Jawaban D)

[collapse]

Soal Nomor 8
Jarak kedua titik potong kurva $y=2^{2x+1}-5\cdot 2^x+2$ dengan sumbu-$X$ adalah $\cdots \cdot$
A. $2$                     C. $4$                    E. $6$
B. $3$                     D. $5$

Pembahasan

Diketahui $y=2^{2x+1}-5\cdot 2^x+2$.
Saat grafik fungsi memotong sumbu-$X$, ordinat titik yang dilalui fungsi bernilai $0$, ditulis $y=0$.
Untuk itu, kita peroleh
$\begin{array}{cc}{2}^{2x+1}-5\cdot 2^x+2& =0\\ 2^{2x}\cdot 2^1-5\cdot 2^x+2& =0\\ (2^x{)}^2\cdot 2-5\cdot 2^x+2& =0\end{array}$
Misalkan $2^x=a$, maka didapat
$\begin{array}{cc}2a^2-5a+2& =0\\ (2a-1)(a-2)& =0\end{array}$
Diperoleh $a=\frac{1}{2}$ atau $a=2$.
Substitusi kembali:
$a=2^x=\frac{1}{2}=2^{-1}\Rightarrow x=-1$
$a=2^x=2=2^1\Rightarrow x=1$
Jadi, koordinat titik potong grafik fungsi terhadap sumbu-$X$ adalah $(-1,0)$ dan $(1,0)$.
Jarak kedua titik ini pada bidang Kartesius adalah $1-(-1)=2$
(Jawaban A)

[collapse]

Soal Nomor 9
Daerah hasil dari $y=f\left(x\right)=5+3^{2x-1}$ adalah $\cdots \cdot$
A. $\{y|y<5,y\in R\}$
B. $\{y|y>0,y\in R\}$
C. $\{y|y>5,y\in R\}$
D. $\{y|0<y<5,y\in R\}$
E. $\{y|1<y<5,y\in R\}$

Pembahasan

Diketahui $y=f\left(x\right)=5+3^{2x-1}$.
Daerah hasil dibatasi oleh asimtot datar grafik fungsi.
Perhatikan bahwa rumus fungsi tersebut dapat kita tulis menjadi $3^{2x-1}=5-y$.
Asimtot datar tercapai saat bentuk $a^n=0$ sehingga haruslah
$5-y=0\iff y=5$.
Dengan demikian, grafik fungsi memiliki nilai untuk setiap $y$ terkecuali untuk $y\le 5$.
Jadi, daerah hasilnya adalah $\{y|y>5,y\in R\}$.
(Jawaban C)

[collapse]

Soal Nomor 10
Daerah hasil fungsi $f\left(x\right)=3^{2-9x}-4$ adalah $\cdots \cdot$
A. $\{y|y>-4\}$
B. $\{y|y>-3\}$
C. $\{y|y>0\}$
D. $\{y|y>3\}$
E. $\{y|y>4\}$

Pembahasan

Diketahui $y=f\left(x\right)=3^{2-9x}-4$.
Misalkan $g\left(x\right)=3^{2-9x}$. Perhatikan bahwa $g\left(x\right)$ memiliki asimtot datar $y=0$, yang artinya $g\left(x\right)>0$ untuk setiap $x\in R$.
Untuk itu, $f\left(x\right)=3^{2-9x}-4$ memiliki asimtot datar $y=0-4=-4$, yang artinya $f\left(x\right)>-4$ untuk setiap $x\in R$.
Jadi, daerah hasilnya adalah $\{y|y>-4\}$.
(Jawaban A)

ONTOH SOAL DAN PEMBAHASAN TENTANG EKSPONEN SMA

Widi | Wednesday, 18 January 2017

1.    Bentuk sederhana dari  = ...

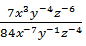Pembahasan:


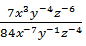
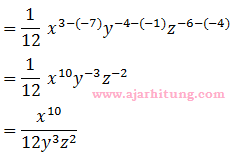
Jawaban: E

2.    Bentuk sederhana dari 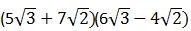adalah ...
a.    22 - 24√3
b.    34 - 22√3
c.    22 + 34√6
d.    34 + 22√6
e.    146 + 22√6
Pembahasan:

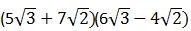
= 30.3 - 20√6+42√6-28.2
= 90 + 22√6 – 56
= 34 + 22√6
Jawaban: D

3.    Bentuk sederhana dari 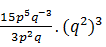 adalah ...

Pembahasan:

Jawaban: B

4.    Bentuk sederhana dari  = ...

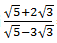Pembahasan:

Jawaban: E

5.    Jika =⋯
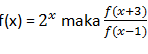a.    f (2)
b.    f (4)
c.    f (16)
d.    f ((x+3)/(x-1))
e.    f (2x + 2)
pembahasan:
karena =

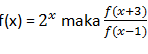Karena 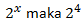 dengan x = 4 atau f(x) = f(4)
Jawaban: B

6.    jika diketahui x = 1/3, y = 1/5, dan z = 2 maka nilai dari 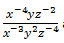adalah ...
a.    32
b.    60
c.    100
d.    320
e.    640
Pembahasan:


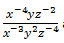
Jawaban: B

7.    Diketahui a = 4, b = 2, dan c = ½. Nilai = ...
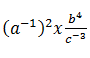a.    ½
b.    ¼
c.    1/8
d.    1/16
e.    1/32
Pembahasan:


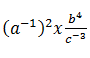
Jawaban: C

8.    Jika , maka nilai x + y = ...
a.    21
b.    20
c.    18
d.    16
e.    14
Pembahasan:

      x-y=4 ...(ii)
Eliminasikan persamaan (i) dan (ii)

subtitusikan y = 8 dalam persamaan x – y = 4
x – 8 = 4
x = 12
sehingga nilai x + y = 12 + 8 = 20
jawaban: B

9.    Dalam bentuk pangkat rasional  = ...

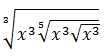Pembahasan:

 

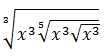
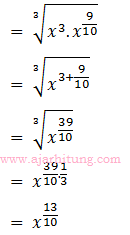
Jawaban: C

10.    Jika x > 0 dan x ≠ 1 memenuhi 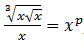, p bilangan rasional, maka p = ...
a.    -1/2
b.    -1/3
c.    1/3
d.    ½
e.    2/3
Pembahasan:


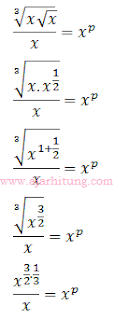
jawaban: A

11.    Nilai yang memenuhi persamaan 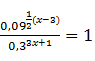 adalah ...
a.    -2
b.    -1
c.    0
d.    1
e.    2
Pembahasan:

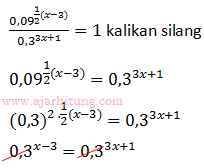
       x – 3 = 3x + 1
      -2x = 4
       x = -2
jawaban: A

12.    Jika bilangan bulat a dan b memenuhi 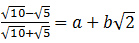 maka a + b = ...
a.    0
b.    1
c.    2
d.    3
e.    5
Pembahasan:

       3 - 2√2= a+b√2
        a = 3, dan b = -2
sehingga nilai a + b = 3 + (-2) = 1
jawaban: B

13.    Jika 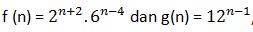, n bilangan asli maka (f(n))/(g(n))=⋯
a.    1/32
b.    1/18
c.    2/9
d.    1/27
e.    1/9
Pembahasan:

Jawaban: D

14.    Nilai x yang memenuhi 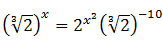 adalah ...
 
Pembahasan:

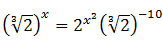
       (3x + 5) (x – 2) = 0
       x = -5/3 atau x = 2
jawaban: C

15.    Nilai a + b, jika 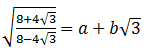 adalah ...
a.    1
b.    2
c.    3
d.    4
e.    5
Pembahasan:


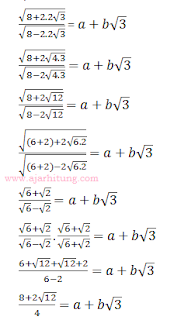
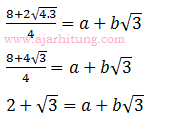
      a = 2, dan b = 1
nilai a + b = 2 + 1 = 3
jawaban: C

16.    anggota himpunan penyelesaian dari persamaan 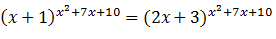  adalah ...
a.    7
b.    4
c.    -4
d.    -7
e.    -11
Pembahasan:


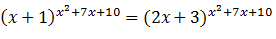
      x+1=2x+3
     -x = 2
      x = -2
dari 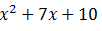dengan x = -2 diperoleh:

Maka:
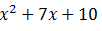= 0
   (x + 2) (x + 5) = 0
    x1 = -2 dan x2 = -5
jadi, jumlah akar-akarnya = -2 + (-5) = -7
jawaban: D

17.    Jumlah akar-akar persamaan 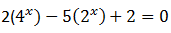 adalah ...
a.    -2
b.    -1
c.    0
d.    1
e.    2
Pembahasan:


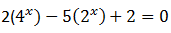
Misalkan, 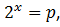 maka: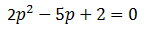

     (2p – 1) (p – 2) = 0
     p = ½ atau p = 2
untuk p = ½, maka 
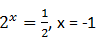
untuk p = 2, maka 
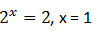
jadi, jumlah akar-akarnya adalah -1 + 1 = 0
jawaban: C

18.    Nilai-nilai x yang memenuhi persamaan 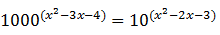 adalah ...
a.    x1 = 1; x2 = 9/2
b.    x1 = -1; x2 = 9/2
c.    x1 = -1; x2 = 7/2
d.    x1 = 1; x2 = -7/2
e.    x1 = -1/2; x2 = 9
pembahasan:


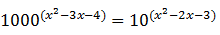
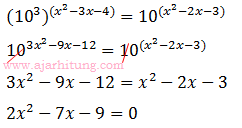
     (2x-9)(x+1)=0
     x = 9/2 atau x = -1
jawaban: B

19.    jika 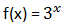maka f(a + 2b – c) = ...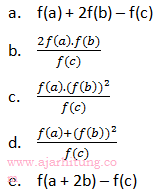
  
pembahasan:


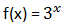
Jawaban: C

20.    diketahui 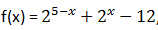, jika f(x1) = f(x2) = 0, maka x1.x2 = ...
a.    6
b.    5
c.    4
d.    -5
e.    -6
Pembahasan:


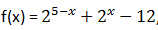
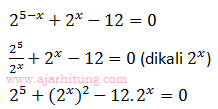
Misal 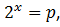maka: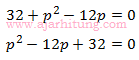

     (p – 8) (p – 4) = 0
      p = 8 atau p = 4
untuk p = 8, 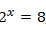, maka x = 3
untuk p =4, 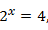, maka x = 2
jadi nilai x1.x2 = 3.2 = 6
jawaban: A

21.    Himpunan penyelesaian 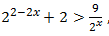 , x ∊ R adalah ...
a.    {x∣-1<x<2}
b.    {x∣-2<x<1}
c.    {x∣x<-1 atau x>2}
d.    {x∣x<-2 atau x>1}
e.    {x∣x<0 atau x>1}
Pembahasan:


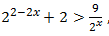
Misal: 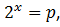 maka:

     (2p – 1) (p – 4) > 0
     p = ½ dan p = 4
untuk p = ½, maka 
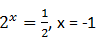
untuk p = 4, maka 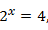, x = 2

HP = {x∣x<-1 atau x>2}
Jawaban: C

22.     = ...
a.    y
b.    x
c.    xy
d.    x/y
e.    y/x
pembahasan:


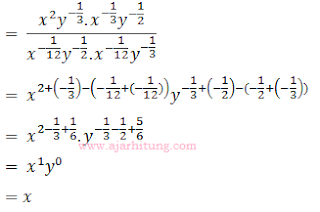
Jawaban: B

23.    himpunan penyelesaian pertidaksamaan 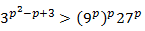 adalah ...
a.    {p∣p< -2- √7  atau p> -2+ √7}
b.    {p∣p<1 atau p>3}
c.    {p∣ -2- √7< p< -2+ √7}
d.    {p∣ 1< p< 3}
e.    {p∣-3< p< -1}
Pembahasan:



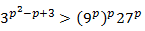
      -√7 < p + 2 < √7
     -2 -√7 < p < -2 +  √7
Jawaban: C

24.    Nilai x yang memenuhi pertidaksamaan 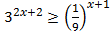 adalah ...
a.    x ≥ -3/2
b.    x ≥ -1
c.    x ≥ 0
d.    x ≥ 1/2
e.    x ≥ 1
pembahasan:


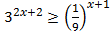
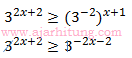
     2x + 2 ≥ -2x – 2
     4x ≥ -4
     x ≥ -1
jawaban: B

25.    diberikan persamaan: 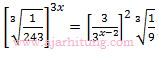jika xo memenuhi persamaan, maka nilai 1 – ¾.xo = ...

Pembahasan:


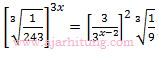
       -15 x = -6x + 18 – 2
       -15 x + 6x = 16
        -9x = 16
         x = -16/9
maka nilai 1 – ¾.xo adalah:

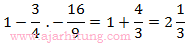
Jawaban: D